在演算法分析中,支配理论(英語:master theorem)提供了用渐近符号(大O符号)表示许多由分治法得到的递推关系式的方法。这种方法最初由Jon Bentlery,Dorothea Haken和James B. Saxe在1980年提出,在那里被描述为解决这种递推的“天下無敵法”(master method)。此方法经由经典演算法教科书Cormen,Leiserson,Rivest和Stein的《演算法导论》 (introduction to algorithm) 推广而为人熟知。
众所周知,递归是算法的一个重要表现形式,不仅作用大,而且其复杂度的分析也比其他方式要繁杂。怎样有效的确定普通递归式和一些典型算法递归式的复杂度,是面试中常常会被问到的。由于递归式复杂度的难以确定,所以目前常用的方法有这么几种:代换猜测法、递归树法、主定理、直接数学分析法。
代换猜测法通常和递归树法合用,利用递归树法得到一个大概正确的结果,然后利用数学归纳法对其验证。
直接的数学分析法相对很直接,很强大,但是对数学要求很高。
在算法分析中,主定理(master theorem)提供了用渐近符号表示许多由分治法得到的递推关系式的方法。主定理通常可以解决如下的递归表达式:
T(n)=a*T(n/b)+f(n)
主定理
首先,是符号的解释:
- 符号Θ,读音西塔,既是上界也是下界,等于,严格贴紧。
- 符号𝑂,读音殴,表示上界,小于等于,贴紧未知。
- 符号𝑜,读音也是殴,小于,不贴紧。
- 符号Ω,读音偶眯嘎,表示下界,大于等于,贴紧未知。
- 符号𝜔,读音也是偶眯嘎,表示下界,大于,不贴紧。
上面的“贴紧”是tight翻译过来的,大概就是是否严格等于的意思吧。
意思就是Θ是平均时间复杂度,𝑂是最坏情况下的复杂度,Ω是最好情况下的复杂度。
下面是主定理,来源维基百科

常见应用
对于应用主定理来说,一定要分清选取定定理中的哪种情况(如果有符合的)。下面是常见的几种应用:
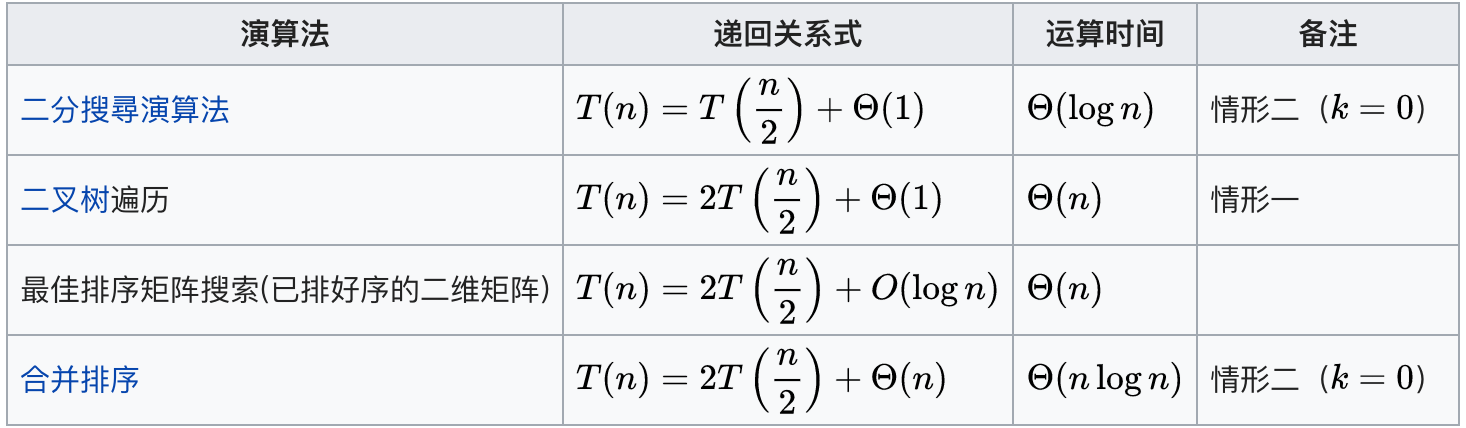
对于复杂的递归,可以先找准递归关系式,再用上面三种情况带入来计算时间复杂度。对于一般的面试已经足够用了。
本文内容整理于网络
今天的内容就到这了,如果觉得对你有帮助的话,请关注我的微信号,让我们共同成长进步~

本文作者:Jessychen
版权声明:本博客所有文章除特别声明外,均采用CC-BY-NC-SA 4.0 Int'l许可协议
如需转载,烦请注明出处: